Bivalue Universal Grave

A Bivalue Universal Grave or BUG is a state of the grid in which every unsolved cell has 2 candidates, without the presence of Hidden Singles.

This is one of the Deadly Patterns that do not occur in a valid Sudoku.

For some people, it is also a solving technique. The aim of this technique is to avoid a BUG pattern, by avoiding moves that would cause it to appear.

Proof of non-uniqueness

In a BUG, each unsolved cell has two candidates, and in each row, column and box constraint, each candidate value occurs exactly twice. If we can find a valid solution using half the number of remaining candidates, all the eliminated candidates would also satisfy each constraint exactly once. This other half will also give us a solution to the puzzle. There is also the possibility that the puzzle does not have a solution at all. In that case, the puzzle is also invalid. The existence of the BUG pattern allows us to conclude that the puzzle is invalid. It has either no solution or 2 solutions.

Assuming uniqueness

When your aim is to prove that the Sudoku has a unique solution, finding a BUG means that you can stop trying. For you, there is no other use for the BUG pattern.

When you trust the maker of the puzzle, who has guaranteed that it has a unique solution, you can use techniques that will prevent the pattern from being formed. Note, however, that since the BUG pattern cannot occur in a well-formed puzzle, such a configuration can also be solved using coloring techniques without having to exploit the solution's uniqueness.

How it works

The whole idea of this solving technique is that if we have a grid that is formed by a BUG grid plus extra candidates, then at least one of the extra candidates must be placed. The term BUG+k is used to denote a BUG grid with k extra candidates. The simplest form is BUG+1, where the sole extra candidate can be immediately placed in its cell.

BUG+1 example

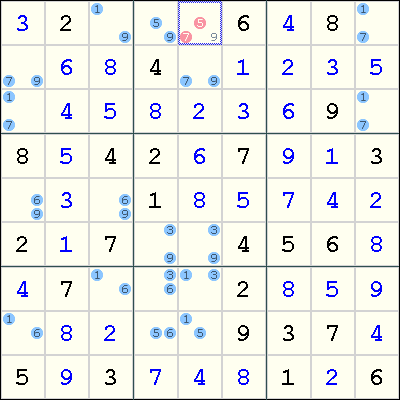
Bivalue Universal Grave, How to solve sudoku puzzles - Solving sudoku strategy,picture 1

This example shows a BUG+1, where the extra candidate is the digit 9 in r1c5. If r1c5 is not 9, then we obtain the BUG pattern. Therefore, 9 can be placed in that cell, and the Sudoku can be solved easily using singles.

As noted above, the same deduction can be made by coloring. Specifically, the chain

r1c3=9 => r7c3=1 => r7c5=3 => r6c5=9

leaves no candidates for digit 9 in box 2.

BUG+2 example

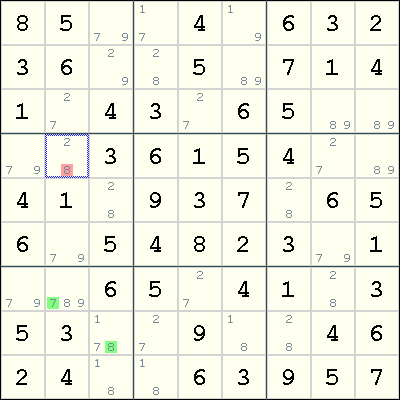
Bivalue Universal Grave, How to solve sudoku puzzles - Solving sudoku strategy,picture 2

This is a case of BUG+2, where the extra candidates are 7 in r7c2 and 8 in r8c3. This implies that either r7c2=7 or r8c3=8. By the following Forcing Chains:

r7c2=7 => r3c2=2 => r4c2=8 r8c3=8 => r5c3=2 => r4c2=8

we deduce that r4c2=8.

Actually, for this example, a much simpler deduction can be made. Because r7c2 and r8c3 see each other, we can immediately conclude that r7c2<>8 and r8c3<>7 (by a simple proof by cases).

Sudoku Games

Free Sudoku Script for Your Website

Sudoku strategies

Printable Sudoku

Sudoku Links