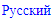XY-Wing

An XY-Wing is a solving technique that uses a short chain of 3 cells.
The cell in the center is called the pivot. The other 2 cells are the pincers.
The chain uses only 3 digits, symbolically named X, Y and Z. Any 3 digits can replace these letters. The pivot contains candidates XY, which explains the name of this technique. The pincers have candidates XZ and YZ.
Any cell that can see both pincers can not longer contain a candidate for digit Z, because the pivot forces either of the pincers to contain this digit.

Subtypes

Although the logic behind the XY-Wing is always the same, subtypes have been introduced to help players to recognize these patterns more easily.
Type 1 (box-line)
One of the pincers shares a row or column with the pivot, the other shares a box. Up to 5 eliminations are possible in this formation.

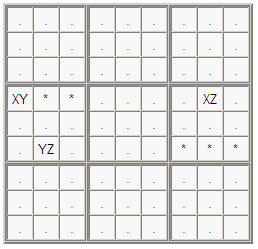
XY-Wing, How to solve sudoku puzzles - Solving sudoku strategy,picture 1

Type 2 (row-column)
One of the pincers shares a row with the pivot, the other shares a column. Only one elimination can be made.

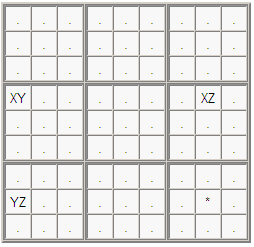
XY-Wing, How to solve sudoku puzzles - Solving sudoku strategy,picture 2

Chain Notation
An XY-Wing is a short chain. You can write it like this in Eureka notation:
(Z=Y)r6c1-(Y=X)r4c1-(X=Z)r4c8
In Nice Loop notation, you must include the cell(s) with the eliminated candidates to complete the loop:
[r6c789]-Z-[r6c1]-Y-[r4c1]-X-[r4c8]-Z-[r6c789] => [r6c789]<>Z

Example

See the following position: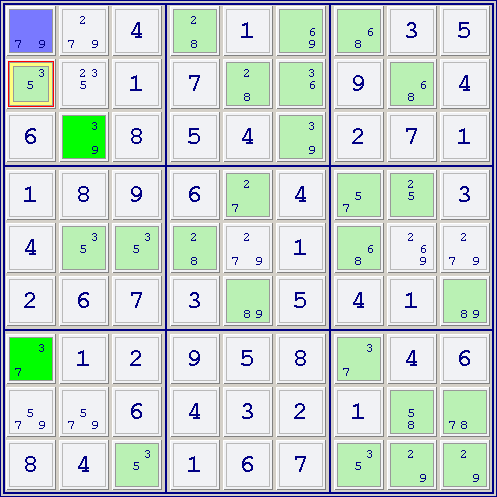
XY-Wing, How to solve sudoku puzzles - Solving sudoku strategy,picture 3

The pivot is R1C1 (blue cell). It has as candidates 79 (XY). The pincers are the green cells: R3C2 (93 or YZ) and R7C1 (37 or ZX).

You can eliminate candidate "3" (Z) from all cells seen simultaneously by both pincers, in this case R2C1. The other possible cells involved are R3C1, R7C2, R8C2 and R9C2 but none of them have a "3" as candidate.

Sudoku Games

Free Sudoku Script for Your Website

Sudoku strategies

Printable Sudoku

Sudoku Links