Kraken Fish
A Kraken Fish is a fish pattern which is connected to a candidate elimination cell (CEC) in such a way that placing this candidate would reduce the secondary set to a size smaller than the defining set.
Here is a diagram depicting a Kraken X-Wing. It has 2 CECs.
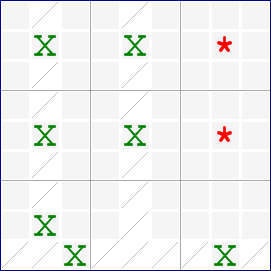
There is a potential X-Wing in columns 2 & 5 and rows 2 & 5. The candidate in r8c2 acts as a fin, but because it does not share a box with one of the candidate forming the X-Wing, it does not cause any eliminations that would normally occur in a Finned X-Wing. The pattern has 2 columns covering 3 rows.
Now consider what would happen if either r2c8 or r5c8 would contain digit X. Both would eliminate all candidate on their own row and through the strong link in row 9, the candidate in r8c2, leaving a pattern with 2 columns covering 1 row, an impossible situation.
Connection Types
In the example, the CECs are connected to the pattern with a direct weak link and an indirect connection via a strong link. However, there are several other methods to connect the CEC to the fish pattern.
- Strong links
- Grouped strong links
- Almost Locked Sets
As a result, the CEC does not even need to be a candidate for the same digit as the pattern. The following diagram shows how an X-Wing pattern for digit X can eliminate a candidate for digit Y.
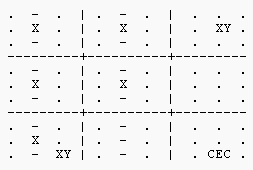
In this example, a similar Finned X-Wing is present, but r2c8 and r9c3 are both bivalue cells with candidates XY. Placing Y in the CEC at r9c8 would force both these cells to X and reduce the fish pattern to a single row and 2 columns.
Sudoku Games
Free Sudoku Script for Your Website
Sudoku strategies
- Coloring
- Singles
- Fish
- Chains and Loops
- Intersections
- Subsets
- Wings
- Single Digit Patterns
- Uniqueness
- Almost Locked Sets


Printable Sudoku
- Kids Sudoku Puzzles
- Easy Sudoku Puzzles
- Standard Sudoko Puzzles
- Hard Sudoku Puzzles
- Expert Soduko Puzzles
- Extreme Soduku Puzzles
- Blank Sudoku Grids

Sudoku Links