Multi-Colors
Multi-Colors is a subtype of coloring that uses more than 2 colors, as opposed to Simple Colors.
This is a single-digit technique. The player first chooses a digit, locates all the conjugate pairs in the grid and starts coloring them. When a candidate belongs to multiple conjugate pairs, all the candidates it is linked to will have the same color, which is the opposite color to that of the candidate itself. Thus, a cluster of candidates is formed. Each cluster must only contain conjugate pairs and has therefore only 2 colors. The colors represent the parity of the candidates in the cluster.
Multi-Colors uses multiple clusters. However, it is not fundamentally different from Simple Colors. Most players just start coloring to see what it may yield. If a move is discovered that requires only a single cluster, then we call it Simple Colors, otherwise we call it Multi-Colors. It is not sensible to start all over again for MC.
When 2 candidates in 2 clusters are peers, they cannot both be true at the same time. In coloring terms, we say that these colors are mutually exclusive. In chaining terms, we say that there is a weak link between these candidates. Another way to say it is that a bridge connects these clusters.
A simple example:
A--------B:
:
C------D
There are 2 conjugate pairs: A-B and C-D. A is weakly linked to C. They cannot be true at the same time. As a result, either B or D must be true, but they could also both be true. They are a connected pair. Any candidate which can see both of them can now be eliminated. Another name for a move of this type is Color Wing.
Multi-Colors have the same power as X-Chains.
Example 1
The first example below looks at the candidates for digit 8.
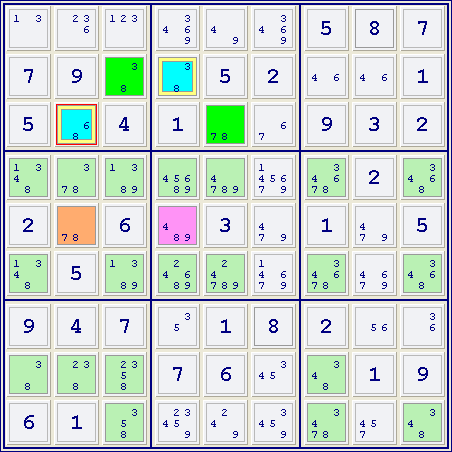
Observe that a blue cell (r3c2) of cluster #1 sees a brown cell (r5c2) of cluster #2, and another blue cell (r2c4) sees a purple cell (r5c4) from cluster #2. Since either the brown cells or the purple cells must contain the digit 8, it follows that the digit 8 can be eliminated from all the blue cells. Hence, the digit 8 can be placed in all the green cells.
Example 2
The second example below looks at the candidates for digit 2.
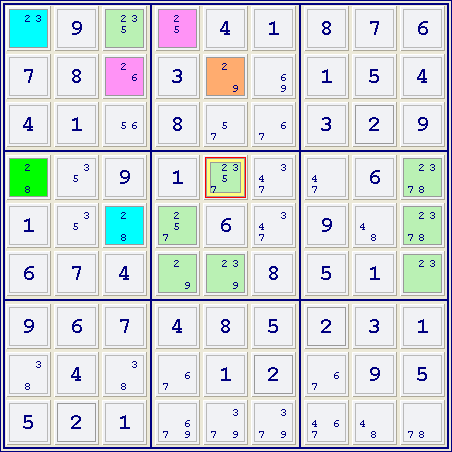
A blue cell (r1c1) of cluster #1 sees a purple cell (r1c4) of cluster #2. This implies that the blue cells and the purple cells cannot both contain the digit 2, which means that either the green cells or the brown cells contain the digit 2. Hence any cell that is seen by some green cell and some brown cell cannot contain the digit 2. This explains the elimination of digit 2 from r4c5.
Sudoku Games
Free Sudoku Script for Your Website
Sudoku strategies
- Coloring
- Singles
- Fish
- Chains and Loops
- Intersections
- Subsets
- Wings
- Single Digit Patterns
- Uniqueness
- Almost Locked Sets


Printable Sudoku
- Kids Sudoku Puzzles
- Easy Sudoku Puzzles
- Standard Sudoko Puzzles
- Hard Sudoku Puzzles
- Expert Soduko Puzzles
- Extreme Soduku Puzzles
- Blank Sudoku Grids

Sudoku Links